A framework for the timely calculation of Swiss producer prices

[ #R #applied macroeconomics #time-series ]

Producer prices in Switzerland, represented by the monthly Producer Price Index (PPI) of the Swiss Federal Statistical Office (FSO), are lagged. On the one hand, price surveys of companies are conducted only every second or every third month, sometimes even only semi-annually or annually. If no survey is conducted in a month, the value of the previous month is adopted. On the other hand, there are sectors where surveys are conducted in the first quarter of the year, for example, but the results are only included in the index one month later. Under the (plausible) assumption that prices are rigid and basically do not change very quickly, this procedure works quite well. However, there are always events that cause prices to change quickly. For example, when the Swiss National Bank abolished the minimum exchange rate against the euro and the Swiss franc appreciated strongly. Also currently the strong increase in oil prices caused by the Covid-19 crisis on the one hand and the Ukraine war on the other hand might lead to quicker than normal changes of prices. In such situations, the approach of the FSO has the consequence that the PPI reflects the actual price development with a delay. Here, I present a framework to overcome these problems and calculate a more timely PPI. The code for the calculations and regularly updated data can be found on github.

I provide a framework to solve the above problems. Instead of adopting the value of the previous month, I estimate a more realistic value using various statistical methods. In addition, I lag some of the indicators to account for the fact that survey data are incorporated later. The timely PPI calculated in this way differs considerably from the original PPI. The difference in the annual inflation rate differs by almost 2 percentage points (March 2015, see Figure above). In April 2021 the difference was around 1 p.p. Moreover, the timely PPI inflation significantly leads original PPI inflation (See Figure below). There is both a significant coincident correlation as well as a significant correlation with a lag of three months with the timely index. The provided timely indices start in December 2010. To simplify life, only the series that are available over the whole sample are used. The others end up in the “rest” residual as I describe below. It would in principle be possible to apply the methodology even further back. However, in 2010 the FSO has changed it’s NOGA classification. So a series named 0.1.11 before 2010 is not necesarily the same series after 2010. Hence, this would require an accurate mapping between the pre and post 2010 series.

Cross correlation

To navigate through the different series and view the methods used, I have developed a web application that can be accessed at the following link (if it does not work, the free monthly time is exhausted): mxbu.shinyapps.io/ppiapp/. I hope this timely index and it’s components might be useful for researchers and policymakers. Let me now provide more details on the calculations.

Tree structure of PPI

The PPI is calculated from five weighted components, which are themselves calculated from weighted components. The granularity consists of a total of six levels. However, the price surveys are only performed for the lowest category (leaf nodes). A natural approach is therefore to represent the PPI in a tree structure (using the R package data.tree), calculate a timely index for the leaf nodes and then aggregate to the other levels up to the PPI. To illustrate the tree structure, here is an example of how the index for A Agricultural and forestry products is constructed.

Tree

It is noticeable that some nodes are labeled with “rest”. This is due to the fact that the FSO does not publish all collected price indicators. However, we know the weight of the published series in the overall index and can therefore calculate a residual, which is labeled with “rest”. Since 2010, the FSO updates the weighting every five years in December. Therefore, it is possible that there is a “rest” series for the period 2010 to 2015, for example, but not from 2015 to 2020. In this case, the series from 2015 to 2020 consists of nothing but zeros.

Erhebungsplan

Methodology

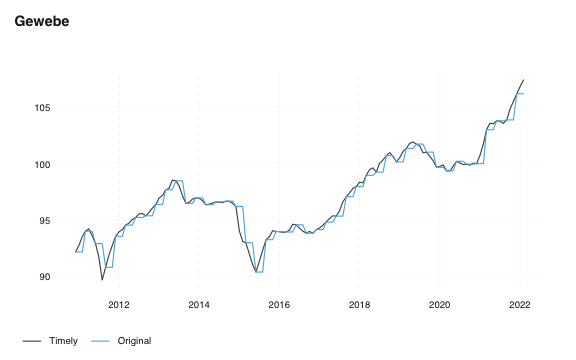
In the next step, a more timely index is created for all leaf nodes (including “rest” nodes). The FSO states that the surveys are carried out regularly (see above the extract from the plan). The idea was therefore to estimate a monthly series using temporal disaggregation (See Chow-Lin, 1971¹) with exchange rate and oil price as indicators. Unfortunately, things look different in the data. For most series, prices change very irregularly which makes the use of the Chow-Lin method impossible. In such cases, the desired values are interpolated. Fortunately, there are still some series that are collected with the regularity indicated by the FSO. In these cases, Chow-Lin can be applied. A nice example is the index for tissue (see below). We see in the disaggregated series that the index dropped sharply both just before the introduction of the minimum exchange rate and after its removal. Economically, this makes sense, moreover, the exchange rate is strongly significant. It is not possible to use the above methods at the current edge. Therefore, timely values are forecasted using an ARIMAX model with exchange rate and oil price as exogenous variables. This might lead to slight revisions at the current edge.

plot of gewebe

Framework

The timely PPI calculation requires several steps

Set up the data tree:

# Load required packages
library(stringr)
library(readxl)
library(tidyverse)
library(tsbox)
library(tstools)
library(tempdisagg)
library(imputeTS)
library(forecast)
library(data.tree)
library(quantmod)
source("utils.R") # This file is on GitHub

#### Update data from Excel?
# This need to be run once a month (when FSO releases new data)
update_excel <- T
if (update_excel) {
source("load_data.R") # This file is provided on GitHub
}
  
# Load PPI 2020
load("PPI_2020.RData") # This file is provided on GitHub

# Load configuration (specifies how to deal with which series)
load("custom_config.RData") # This file is provided on GitHub

# Get level (depth) of series
ppis_level_nr <- as_tibble(lapply(ppis_level.2020, function(x) {
  which(as.logical(x))
}))

# Get series names
ppis_names <- as_tibble(lapply(ppis_level_names.2020, function(x) {
  x[which(!is.na(x))]
}))

# Set up tree
nmes <- colnames(ppis_level.2020)
tree <- Node$new("PPI")
sapply(c("A", "B", "C", "D", "E"), function(x) tree$AddChild(x))

for (ii in 1:length(nmes)) {
  if (ppis_level_nr[ii] != 1) {
    pn <- find_parent(colnames(ppis_level_nr[ii]), ppis_level_nr)
    FindNode(tree, pn)$AddChild(colnames(ppis_level_nr[ii]))
  }
}

2.Assign initial series and weights to tree and implement shift if needed:

ppis.2010$PPI <- PPI.2010
ppis.2015$PPI <- PPI.2015
ppis.2020$PPI <- PPI.2020
# Assign initial series and weights to tree & implement shift if needed
tree$Do(function(x) {
  x$fullName <- ppis_names[[x$name]]
  x$w.20 <- round(as.numeric(ppis_weights.all[[x$name]][1]), 4)
  x$w.15 <- round(as.numeric(ppis_weights.all[[x$name]][2]), 4)
  x$w.10 <- round(as.numeric(ppis_weights.all[[x$name]][3]), 4)
  if (x$name == "21.1"){# Pharmazeutische Grundstoffe Shift
    x$TSI.20 <- round(ts(ppis.2020[[x$name]], start = c(2020, 12), frequency = 12), 4)
    x$TSI.15 <- round(ts(ppis.2015[[x$name]], start = c(2015, 12), frequency = 12), 4)
    x$TSI.10 <- round(ts(ppis.2010[[x$name]], start = c(2010, 12), frequency = 12), 4)
    x$ORIG <- ts_chain(x$TSI.20, x$TSI.15) %>% ts_chain(x$TSI.10)
    x$FTSI <- shift_time(x$ORIG, 2, 2010)
  }
  else if (x$name == "21.2"){# Pharmazeutische Spezialitäten Shift
    x$TSI.20 <- round(ts(ppis.2020[[x$name]], start = c(2020, 12), frequency = 12), 4)
    x$TSI.15 <- round(ts(ppis.2015[[x$name]], start = c(2015, 12), frequency = 12), 4)
    x$TSI.10 <- round(ts(ppis.2010[[x$name]], start = c(2010, 12), frequency = 12), 4)
    x$ORIG <- ts_chain(x$TSI.20, x$TSI.15) %>% ts_chain(x$TSI.10)
    x$FTSI <- shift_time(x$ORIG, 1, 2010)
  } 
  else if (x$name == "20.14" | x$name == "20.5"){# Chemische Grundstoffe & Andere Shift
    x$TSI.20 <- round(ts(ppis.2020[[x$name]], start = c(2020, 12), frequency = 12), 4)
    x$TSI.15 <- round(ts(ppis.2015[[x$name]], start = c(2015, 12), frequency = 12), 4)
    x$TSI.10 <- round(ts(ppis.2010[[x$name]], start = c(2010, 12), frequency = 12), 4)
    x$ORIG <- ts_chain(x$TSI.20, x$TSI.15) %>% ts_chain(x$TSI.10)
    x$FTSI <- shift_time(x$ORIG, 2, 2010)
  }
  else {# No shift
    x$TSI.20 <- round(ts(ppis.2020[[x$name]], start = c(2020, 12), frequency = 12), 4)
    x$TSI.15 <- round(ts(ppis.2015[[x$name]], start = c(2015, 12), frequency = 12), 4)
    x$TSI.10 <- round(ts(ppis.2010[[x$name]], start = c(2010, 12), frequency = 12), 4)
    x$FTSI <- ts_chain(x$TSI.20, x$TSI.15) %>% ts_chain(x$TSI.10)
    x$ORIG <- ts_chain(x$TSI.20, x$TSI.15) %>% ts_chain(x$TSI.10)
  }
  
},
traversal = "post-order"
)

3.Create rest nodes and calculate rest series:

# create nodes with rest
for (ii in 6:1) {
  tree$Do(function(x) {
    if (ii == 1) {
      tree$w.20 <- round(Aggregate(x, "w.20", sum, na.rm = T), 4)
      tree$w.15 <- round(Aggregate(x, "w.15", sum, na.rm = T), 4)
      tree$w.10 <- round(Aggregate(x, "w.10", sum, na.rm = T), 4)
    }
    if (round(Aggregate(x, "w.15", sum), 4) != round(x$w.15, 4) | 
        round(Aggregate(x, "w.10", sum), 4) != round(x$w.10, 4) | 
        round(Aggregate(x, "w.20", sum), 4) != round(x$w.20, 4)) {
      
      nw15 <- round(Aggregate(x, "w.15", sum, na.rm = T), 4)
      nw10 <- round(Aggregate(x, "w.10", sum, na.rm = T), 4)
      nw20 <- round(Aggregate(x, "w.20", sum, na.rm = T), 4)
      
      # Add new child ".rest"
      x$AddChild(paste(x$name, ".rest", sep = ""))
      nnode <- FindNode(tree, paste(x$name, ".rest", sep = ""))
      nnode$fullName <- paste(x$name, ".rest", sep = "")

      nnode$w.20 <- round(x$w.20, 4) - nw20
      nnode$w.15 <- round(x$w.15, 4) - nw15
      nnode$w.10 <- round(x$w.10, 4) - nw10
      
      # If weights do not add up to 1, calculate rest series
      TSR <- getRest(x, x$children)
      nnode$TSI.10 <- TSR$TS.10
      nnode$TSI.15 <- TSR$TS.15
      nnode$TSI.20 <- TSR$TS.20
      
      # Chain rest series
      cR <- chainRest(x, TSR)
      nnode$ORIG <- cR$ORIG
      nnode$FTSI <- cR$FTSI
      
    }
  },
  traversal = "post-order",
  filterFun = function(x) {
    x$level == ii & !x$isLeaf
  }
  )
}

4.Remove repeating values (indicating that there was no survey in this month):

# Remove stair values
tree$Do(function(x) {
  message(x$name)
  x$TSI.ND.20 <- remove.double(x$TSI.20)
  x$TSI.ND.15 <- remove.double(x$TSI.15)
  x$TSI.ND.10 <- remove.double(x$TSI.10)
  x$FTSI.ND <- remove.double(x$FTSI)
},
traversal = "post-order"
)

5.Calculate timely series for leaf nodes:

# Load exogenous variables (Oil price, nominal exchangerate, trend)
exo_raw <- ts_fred(c("WTISPLC", "EXSZUS", "NBCHBIS")) %>% ts_ts()
exo_raw <- window(exo_raw, start = c(2010,1), end=c(actual_y,actual_m))
exo <- ts_tbl(exo_raw) %>%
  ts_wide() %>%
  mutate(neer = NBCHBIS) %>%
  mutate(oil =  WTISPLC*EXSZUS) %>%
  select(c("time", "neer", "oil")) %>% #chfeur
  ts_long %>% ts_ts()
trend <- ts(1:((actual_y-2010-1)*12+1+actual_m),start =c(2010,1), end=c(actual_y,actual_m), frequency = 12)

# Calculate timely values and assign series to leaf nodes
tree$Do(function(x) {
  print(paste0("Calculate timely series: ", x$name))
  if (sum(is.na(x$FTSI.ND)) >= 1) {

    # Use predefined method to interpolate 
    AC <- AssignCustom(x, config, exo, trend, actual_y, actual_m)
    x$FTS.C <- AC$ts
    x$FTS.MOD.TD <- AC$mod.td
    x$FTS.MOD.AR <- AC$mod.ar
  } 
  else {# If no missing values
    x$FTS.C <- x$FTSI.ND
    x$FTS.C <- x$FTS.C / window(x$FTSI, start = c(2020, 12), end = c(2020, 12))[[1]] * 100
  }
  },
traversal = "post-order",
filterFun = function(x) {
  x$isLeaf
}
)

6.Finally, aggregate series to PPI and components:

# Aggregate PPI
for (ii in 6:1) {
  tree$Do(function(x) {
    print(paste0("Aggregate: ",x$name))
    
    # Aggregate original series (as Control)
    TS.AG <- AggregateOrig(x$children)
    x$FTS.AG <- TS.AG$FTS
    x$TS.AG.10 <- TS.AG$TS.10
    x$TS.AG.15 <- TS.AG$TS.15
    x$TS.AG.20 <- TS.AG$TS.20
    
    # Aggregate interpolated series 
    TS.C <- AggregateCustom(x$children)
    x$FTS.C <- TS.C$FTS
  },
  traversal = "post-order",
  filterFun = function(x) {
    x$level == ii & !x$isLeaf
  }
  )
}

We end up with a tree object with the name “tree”, which contains all relevant information. The tree object can be moved along with the $ sign: tree$C$21.2. Each “node” of the tree has the following important attributes:

-$isLeaf: TRUE = index has no subcomponents.

-$FTSI: original series of the FSO.

-$FTSI.ND: original series of the OFS, non-changing values are set to NA.

-$FTS.C: Calculated timely series.

-$FTS.AG: As control: all original series are aggregated (must be equal to FTSI).

-$FTSI.MOD.TD: if isLeaf = TRUE, model of TD.

-$FTSI.MOD.AR: if isLeaf = TRUE, model of ARIMAX to update at current edge.

Tweaks

Since some things seemed implausible, the following tweaks were made:

-Looking at the index for “pharmaceutical specialties” and “steel and light metal construction” (21.2 and 25.1) it is noticeable that from 2016 onwards there is still a step function even after removing non-chaniging values. This might be because small companies report their prices monthly while the large companies report quarterly. The reports of small companies change the index 2 digits behind the decimal point. I think these small changes are negligible and not realistic and are therefore re-estimated.

-In contrast to the temporally disaggregated series, the indices that are interpolated cannot reflect the Swiss franc shock of 2015. This is taken into account by setting the December value of these series to that of the last change.

-At the current edge, the values are updated with an ARIMAX model to avoid the step function here as well.

-All indices are set to 100 in December 2020. This might lead to a “shift”.

Chow, G. C., & Lin, A. L. (1971). Best linear unbiased interpolation, distribution, and extrapolation of time series by related series. The review of Economics and Statistics, 372-375. ↩

A framework for the timely calculation of Swiss producer prices

Tree structure of PPI

Methodology

Framework

Tweaks

Comments You need to have a GitHub Account to comment!

Comments